(c) 2001, Stephen E. Sachs <contact me>
‘Intensional’ Aspects of Names in Russell and
Frege
by Stephen E. Sachs
Philosophy 141: Frege, Russell, and the Early Wittgenstein
Oystein Linnebo, TF
January 12, 2001
In forming their theories for understanding propositions, both Gottlob
Frege and Bertrand Russell were forced to address basic questions
regarding the role of names. Do names serve only as placeholders to
denote certain entities, or is there something logically significant about
exactly how the names pick out the entities with which they are
associated — about their mode of presentation? The names
“The present Pope” and “John Paul II” seem to have
a difference that goes beyond their different grammatical form; yet that
difference cannot be thought to be so stark as to prevent them from
denoting the same object. How is it that the specific choice of name
can affect one’s understanding of the proposition?
To
Frege, the mode of presentation was certainly a significant aspect; in fact, he
gave the mode of presentation a fundamental place in his ontology as the
“sense” of the name, distinct both from its denotation and from the
subjective ideas associated with the word.[1] Russell, however, rejected the concept
of sense and placed far less emphasis on what I will call the “intensional”
aspects of names — the properties that they do not share with other names
that denote the same entity.[2] Instead, Russell chose to analyze the
proposition containing the name, eliminating (or, perhaps making explicit) the
intensional aspects of names through a process that showed radical
differences between grammatical and logical form. Yet Russell’s success in analyzing away the
intensional aspects of names is anything but clear; the possibility of
informative identities among sense-data or sensory universals poses a number of
severe difficulties to his theory, and even if the theory is consistent,
Russell’s process of analysis seems to remove all useful methods for the
communication of thoughts.
Intensional
aspects can become relevant in distinguishing among names in two ways. Since there is no danger of confusing names that denote different objects, intensional aspects are necessary only to
resolve questions where two names denote the same object or where both names
fail to denote any object at all.
Concerning the latter, if the means by which a name indicates its object
is irrelevant, then all vacuous names — expressions whose grammatical
form makes it seem that they denote an object, yet in fact fail to do so
— must be, in some sense, equivalent. Examples include proper names such as “Odysseus”
or definite descriptions like “the present king of France”; they
also include pieces of pure nonsense such as “Hrzbk.” However, although both types of names
are equally vacuous, the expressions of the former category seem somehow more
meaningful than those of the latter. A robust logical theory should give
content to this distinction and should also allow us to decide the status of
propositions containing such expressions, such as “the king of France is
bald” — a proposition which seems to generate contradictions if it
held to be either true or false.
If
we are to distinguish between “the present king of France” and
“the present zorg of Blaxon,” something intensional that relates to
the expressions themselves and not the objects they denote must be involved in
their interpretation. For Frege,
this dilemma is easily resolved by the availability of sense; pure nonsense
lacks sense, while “Odysseus” or “the present king of
France” remain meaningful because they have sense even without
denotation. Thus, a proposition
such as “the king of France is bald” takes no truth-value, since
part of that expression is bedeutungslos
and thus prohibits the whole from having a denotation (i.e., a truth-value).[3] Russell, however, who does not allow
for sense or for other intensional aspects, would find Frege’s method
inapplicable to either problem; thus propositions containing seemingly
meaningful descriptions and those containing gibberish would seem to be
indistinguishable.[4]
The
occurrence of vacuous proper names in propositions therefore seems to be fatal
— and so, in the essay “On Denoting,”[5] Russell describes a process of
whereby proper names and descriptions are, to the fullest extent possible,
removed. Indefinite descriptions are analyzed according to
Frege’s quantificational logic;[6] in the case of definite descriptions, a contextual
definition is offered that transforms “Scott is the author of
Waverley” to “there is an x such that x wrote
Waverley and no one else did, and furthermore x was Scott,” a
form in which nothing corresponding to the original description
appears. In general, statements of the form “the F has
G” become 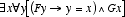 , a structure entirely
without definite descriptions like “the F”; problems of
vacuous descriptions can then be resolved using more familiar logical
techniques. “The present king of France is bald” would become
the sentence
, a structure entirely
without definite descriptions like “the F”; problems of
vacuous descriptions can then be resolved using more familiar logical
techniques. “The present king of France is bald” would become
the sentence 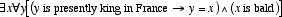 , which, because
there
is no such x, can be clearly determined to be false. To resolve the
status of sentences such as “Apollo is bald,” instances of
“Apollo” can be replaced with a corresponding definite
description — Russell suggests “the sun-god”[7]— and the sentence interpreted
using previously outlined rules. Of course, there is a need for
iteration of this procedure if the definite description contains new
proper names, and there must be a guarantee that the analysis will cease
after a finite number of iterations, but these will be dealt with
below. What is important to note at this point is that as proper
names and definite descriptions are eliminated, the danger of vacuity
disappears, and the dilemmas noted above lose their relevance.
, which, because
there
is no such x, can be clearly determined to be false. To resolve the
status of sentences such as “Apollo is bald,” instances of
“Apollo” can be replaced with a corresponding definite
description — Russell suggests “the sun-god”[7]— and the sentence interpreted
using previously outlined rules. Of course, there is a need for
iteration of this procedure if the definite description contains new
proper names, and there must be a guarantee that the analysis will cease
after a finite number of iterations, but these will be dealt with
below. What is important to note at this point is that as proper
names and definite descriptions are eliminated, the danger of vacuity
disappears, and the dilemmas noted above lose their relevance.
This
process of analyzing sentences until the original names disappear is equally
effective in resolving the two problems in which different names refer to the
same objects: informative identity and “indirect speech.”[8] Frege opens his discussion in
“On Sense and Denotation” by examining the former. He
notes that identity must be a relation between names or signs rather than
objects; one cannot say that two objects are identical, for then they
would be the same object, and the statement “a = b” would seem
to have no more content than “a = a.” Yet statements of
identity do seem to have content; statements like “The Morning Star
= The Evening Star” are by no means a priori.[9] If identity is a relation among names,
however, it must be more than a merely formal relation among marks on
paper; any symbol can be introduced to represent any other, and identity
in such a view could provide only linguistic truths. To cite the
example from Frege’s letter to Philip Jourdain,[10] the statement “Afla = Ateb”
does not tell us that “Ateb” is a symbol for
“Afla,” but that the mountains observed and presented as Afla
and Ateb are in fact the same mountain.[11]
How is informative identity then to be understood? Frege can
explain the difference in “cognitive value” through a
difference in sense, as “Afla” and “Ateb” utilize
different modes of presentation.[12] Russell, however, has no such option, and
must again eliminate the identities in the course of analysis.[13] We have already seen what
would happen to “Scott = the author of Waverley”; in
the case of proper names, Afla and Ateb would be reduced to their
descriptions “the F” and “the G,” which in
Russell’s analysis would eventually reduce their identity to 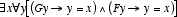 . The only identities here are
between bound
variables, where no mode of presentation is at issue and no issue of
informative identity can arise.
. The only identities here are
between bound
variables, where no mode of presentation is at issue and no issue of
informative identity can arise.
The elimination of informative identity provides for the quick
resolution of the problem of indirect speech on which Russell placed such
emphasis. Russell accepted the principle of indiscernability of
identicals (also called Leibniz’s Law), that if a = b, then a may be
substituted for b in any proposition without loss of truth.[14] However, when such
propositions involve indirect speech — the discussion of one
proposition in another where it is “indifferent to the truth of the
whole whether the subordinate clause is true or false” — this
principle seems to break down.[15] To cite Russell’s favorite example,
the truth of “George IV wished to know whether Scott was the author
of Waverley” is entirely separate from whether Scott indeed
authored Waverley. Yet Scott was the author of
Waverley, which should by substitution should allow us to conclude
that “George IV wished to know whether Scott was Scott,” which
is false.[16]
The
crucial point in this discussion is that for Russell, the problem of
substitution in indirect speech appears only through the use of informative
identities.[17] Consider the statement “George IV
believes A has H.” If I am
to substitute something into that sentence, I must be sure that an identity
exists that justifies the substitution.
Furthermore, that identity may not be merely formal. If I introduce the name “B”
to symbolize A, so that “A = B” is stipulated as true, then
“George IV believes B has H” will, given this symbolism, in fact be
true and cause no contradiction — even if His Royal Majesty would never
have expressed his belief in those exact terms. To create the contradiction, it is necessary to impute a
belief to George IV that he did not have, meaning that the substitution must
contain additional knowledge; without informative identities, the premise of
Leibniz’s Law will never be satisfied. The statement said to be believed by George IV, namely that
“A has H,” will often itself be changed by analysis, and Russell in
“On Denoting” uses this fact, rather than the elimination of
informative identity, to resolve the problems posed by indirect speech; yet
this approach, though correct, is unnecessary. As long as informative identities may be analyzed away,
propositions involving indirect speech will not experience meaningful
substitutions and will pose no danger to the theory of descriptions.
Russell
thus seems secure as long as informative identities may be removed through
analysis. Yet Russell has such
option where the informative identity “A = B” is already fully
analyzed and need not be restated in a different logical form; should such an
identity ever arise, there will be no escape from the contradictions.[18]
The question of whether fully analyzed terms may be found in informative
identities is not, to my knowledge, explicitly addressed by Russell; yet it is
a question of fundamental importance to his theory. If fully analyzed identities can be proven impossible, then
the theory is well-protected from the dangers posed by intensional aspects of names; if such identities can be found to exist, then the theory may well be
inconsistent.
To
determine whether fully analyzed and informative identities exist, it is
necessary to examine the meaning of “fully analyzed.” As stated earlier, the process of
analysis that Russell outlines in “On Denoting” requires, must be
an iterated process; understanding “Aristotle” as “the
student of Plato and teacher of Alexander”[19]
would require descriptions of Plato and Alexander — and so on ad
infinitum, unless there is a basic level at
which the analysis ceases, the full logical structure of the proposition is
revealed, and we may make our judgment as to its truth or falsity. To create this basic level, Russell
introduces the notion of acquaintance:
we are acquainted with certain entities, and those entities with which
we are not acquainted can, after a sufficient amount of analysis, be expressed
in descriptions composed only of entities with which we are acquainted.[20] For brevity, I will speak of “acquainted
entities” and “described entities”: as is clear from the process of analysis, acquainted
entities may be mentioned only through the use of proper names, while described
entities must either begin as definite descriptions or be translated into them.[21]
In
its general sense, Russell gives little explanation of the notion of
acquaintance — among other things, he says one is acquainted with an
object when one has a “direct cognitive relation” to it, but what
cognitive relations may be considered “direct” and what objects
might be termed acquainted depends on his epistemology rather than his logic.[22] From logic’s perspective,
acquaintance serves only as a formal distinction and a terminus in the analysis
of sentences; the proper name of an acquainted entity must not be vacuous, and
whether an entity is acquainted or described must always be decidable, but
otherwise logic imposes no limits on the number or kind of acquainted
objects. If one’s
epistemology allows for direct cognitive relations with angels, then angels may
be considered acquainted entities and one may mention them in fully analyzed
propositions.
We
have already seen that if an informative identity is to be found, it must come
at the level of acquainted entities.
Yet if one chooses an epistemology that allows for knowledge, say, of
angels, what would prevent an informative identity of the form “Angel A =
Angel B”? It would seem that
Russell’s notion of acquaintance must, in order to ensure his
consistency, give content to the notion of “direct cognitive
relation” such that two informative names of acquainted entities are
prevented from referring to the same object.[23] Such a clarification is attempted in The
Problems of Philosophy,[24]
where he states that direct awareness of an entity is awareness “without
the intermediary of any process of inference or any knowledge of truths.”[25] Russell gives as an example a
sense-datum of a certain patch of color; although many things may be said about
it — “that it is brown, that it is rather dark” — those
truths, or others that might later be learned, do not reveal anything in the
sense-datum that was not known before.
His knowledge of the color is perfect and complete, “and no
further knowledge of it itself is even theoretically possible”;
acquainted entities are thus those “immediately known to me just as they
are.”[26]
This
property of complete knowledge is what recommends protects Russell against
informative identities, and his argument that knowledge of sense-data is
complete recommends his empiricist epistemology in which only sense-data can be
acquainted.[27] Identities, to be informative, must
contain information about the entity named that was not known before;
“Afla = Ateb” would be trivial if all of the properties of the
mountain were already assumed when one spoke of it. To claim such complete knowledge for mountains or angels
requires a rather bold epistemology; yet when dealing with a sense-datum, there
seems to be a logical guarantee of complete knowledge. My sense-data are such by virtue of the
fact that I perceive them, and there cannot be any aspect of what I perceive
that I have not yet perceived.
Although my perception of the letters on the eye doctor’s chart
might become more sharp as I squint and pay attention to them, that does not
deprive my earlier blurry perceptions of their status as having been my actual
sense-data.[28]
If
this analysis is correct, then it would seem impossible to show informative
identities among sense-data. Yet
Russell himself recognized that this doctrine of complete knowledge encounters
“some difficulty” concerning the definition of “one sense-datum.”[29] Russell notes that sense-data may be
complex, and that further attention may reveal new information about the
relations among their parts;[30]
however, he gives no means of determining whether a complex sense-datum has
been fully broken into constituents.
A patch of color may be understood as a large number of smaller patches,
and thus be divisible in space; a given sense-datum may seem to persist for a
certain duration, and thus be divisible in time; and if there are in fact
“point-sized” sense-data sufficiently limited in time and space as
to be indivisible, it would be near-impossible for Russell to state what the
appropriate limits might be.[31]
While
this line of approach seeks to restrict the scope of “one
sense-datum,” the need to avoid informative identity makes one wish the
scope expanded. Daily experience
offers us sense-data that are very similar, and it is possible that one might
perceive two sense-data that seem, for all intents and purposes, exactly alike.
They again might be separated in space, as in the case of two patches of white
on a computer screen, or in time, as in the case of sense-data perceived before
and after one blinks. If the perception of the patch of color that constitutes
each of the two sense-data (call them A and B) is precisely identical, then the
distinction between them — the reason “A = B” does not hold
— must lie in the fact that they cannot be substituted for each other in
propositions that discuss their spatial or temporal ordering, such as “A
is before B.”[32] However, such a sense-datum must not be
just the particular patch of color that
is perceived; it must contain information about its relations as well, which is
quite unusual. Given a sense-datum
that is half-red and half-blue, one should be able to speak of a component blue
sense-datum without also mentioning the red adjacent to it or the music that
was playing in the background; one should be able to pick out particular
elements and refer to them as individuals. Yet it now seems that the relations of a sense-datum to its
fellows must be essential and inextricable parts of its character; one may not
speak of sense-datum A without including within it one’s perception
(one’s sense-datum, it would seem) of A’s ordering relative to
other sense-data in time and space.
This lack of independence seems problematic, especially since Russell
describes the process of becoming acquainted with spatial and temporal
relations as one of abstraction from pre-existing sense-data.[33]
Such
concerns may render the presence of informative identities among sense-data
likely, but they do not conclusively establish their existence, relying as they
do upon the ambiguity in the concept of “one sense-datum.” Yet sense-data are not the only
acquainted entities; according to Russell, we are also acquainted with
universals, viewed by Russell as qualities that may be shared by many
particulars.[34] Russell charts the development of a
universal as follows: we begin with
acquaintance with particular yellows, and “if we have seen a sufficient
number of yellows and have sufficient intelligence, we are aware of the
universal yellow.”[35] Given that universals may be subject
terms rather than only predicates, as in Frege,[36]
there seems no reason why they may not be informatively identical — and
there is good reason to think that some are.
If
universals are abstracted from particulars, then any useful sensory universal
must be general enough to include sense-data which we have not yet
perceived. For instance, we may
experience sense-data of shades of color A, B, and C, and later abstract from
them the universal “aquamarine” which means something more than
“exactly resembles either A, B, or C.” Thus other similarities between these three sense-data may
be ignored in the process of forming a specific universal — for instance,
whether they are mottled or smooth, or whether they would be better described
as light aquamarine or dark — and there does not seem to be any clear
limit on how general the abstracted similarities may be. Looking at a group of objects from
which I might abstract “aquamarine,” I could consider more general
similarities and abstract the universal a. I could follow the same process with a
group of objects from which one might abstract “navy” and, at a
higher level of generality, instead abstract the universal b. It seems entirely possible that the
universals I abstract separately from each might in fact be precisely identical
and also identical to “blue” — implying, it seems, that
“a
= b”
is a valid informative identity.[37]
One
might object that a and b ought not be considered identical but merely
coextensive. Russell does allow
for distinct coextensive predicates — in fact, his Axiom of Reducibility
stipulates them — but there seems no good reason to confine observations
of similarity among sensory universals (all of which are of the same type and
order) to coextensionality.
Universals are terms, and it should be possible to use them as
participants in identity relations rather than only in predicative
statements. Any statement I make
about a
would seem to hold equally well of B; the only cases I am aware of in which the
substitution fails would be those of indirect speech, since one may believe
“a
= a“
without holding that “a = b.”[38] To prohibit this use of identity
because it causes contradictions elsewhere in the theory is logically sound but
highly unsatisfying; it smacks of “solving” Russell’s Paradox
by stipulating that only those sets exist whose existence does not lead to a
contradiction. At the same time,
however, this may not be considered a clear refutation of Russell’s
views. There is no guarantee that
universals may in fact be informatively identical — and thus no
conclusion as to whether any intensional aspects of names are required for one
to understand them.
Yet
even assuming that Russell has been successful in eliminating from his system
intensional aspects of names, his success has come at a not insignificant
cost. Frege’s concept of
sense served not only to explain certain puzzles, but also to establish a
public meaning for a word or proposition, something distinct from the
subjective ideas a word may conjure.
In analyzing away all concept of sense, Russell also analyzed away all
objects that could be perceived by more than one individual — all
entities that could be described by Frege’s “common store of
thoughts” shared by mankind.[39] The subjects of fully analyzed
propositions such as “this is yellow” may offer no mode of
presentation, but as a result they make their truth-grounds for anyone but the
speaker utterly obscure.
Constructions of sense-data are unintelligible to those who have not
experienced the same sense-data — and the concept of “same
sense-data” is empty if all informative identities have been
removed. Even if I have
experienced the same “this” as the speaker of “this is
yellow,” without informative identities of universals, I would be forever
uncertain whether the “yellow” mentioned is in fact the universal I
call by that name.[40] Worst of all, if communication of this
sort is prohibited, Russell’s theory itself may not stated in a way that
enables it to be understood.
Although the problems of intensionality cannot show Russell’s
system to be inconsistent, the concessions he makes to avoid contradiction
leave the theory painfully limited and perhaps unsatisfying to those seeking a
means of understanding propositions.
[1] I shall use “denotation” as a translation
of Frege’s bedeutung. The emphasis which Frege placed on
sense is evident from his declaration that “for the purpose of acquiring
knowledge,” the sense of a sentence was to be treated as “no less
relevant than its [denotation], i.e. its truth-value” (“On Sinn and Bedeutung,” 1892, The Frege Reader, ed. Michael Beaney (Oxford: Blackwell Publishers, 1997), p. 171).
[2] I use this term with the strong suspicion that my
usage is incorrect, but its use here seems analogous to its use in specifying
the differences between coextensive concepts; in any case, this understanding
is employed merely to supply a label and not to interpret the use of the word
in other texts.
[3] Of course, the ease with which Frege answers the
present question comes at the cost of much difficulty elsewhere, namely how one
is to know that such statements as “Kepler died in misery” in fact
take a truth-value. (“On Sinn
and Bedeutung,” p. 162) His
conclusion is that the use of such names in a logical statement presupposes
that they denote something, and that such names would be eliminated through the
proper construction of a “logically perfect language” (“On Sinn and Bedeutung,” p. 163). A further
difficulty concerns the exact sense of some proper names; while “the
present king of France” has a clear mode of presentation,
“Aristotle” does not, and Frege is forced to accept that different
people may use the term with a different sense as long as the denotation
remains the same — another issue that “ought not to occur in a
perfect language” (“On Sinn and Bedeutung,” p.
153).
[4] Russell also may not accept the truth-value gap; since
he views propositions as actual objects rather than (as Frege does) names for
The True or The False, he must instantiate laws of logic (such as
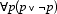 ) with propositions rather than
truth
values, and a
proposition neither true nor false would therefore violate the law of the
excluded middle.
) with propositions rather than
truth
values, and a
proposition neither true nor false would therefore violate the law of the
excluded middle.
[5] Bertrand Russell, “On Denoting,” Mind
n.s. 14 (October 1905), pp. 479-93.
Page citations will be taken from the edition photocopied and handed out
in class.
[6] E.g., “all men are
mortal” becomes 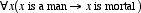 .
.
[7] “On Denoting,” p.
117.
[8] “On Sinn and
Bedeutung,” p. 159.
[9] “On Sinn and
Bedeutung,” p. 151.
[10] Letter to Phillip Jourdain,
Jan. 1914, The Frege Reader, pp. 319-322.
[11] Letter to Jourdain, p.
320-1.
[12] “On Sinn and
Bedeutung,” p. 152.
[13] Cf. Bertrand Russell,
“Knowledge by Acquaintance and Knowledge by Description,”
1910-11, Mysticism and Logic (London: George Allen, 1970) pp.
163-4.
[14] “On Denoting,”
p. 110. The principle may be logically expressed as
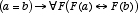 .
.
[15] “On Sinn and
Bedeutung,” p. 160.
[16] “On Denoting,”
p. 110.
[17] For Frege, the problem is
somewhat more severe; since propositions normally denote their
truth-values, it would seem that “George IV believes P” can be
substituted for “George IV believes Q” as long as P and Q are
either both true or both false. Frege therefore introduces the
theory that propositions used in indirect speech denote their usual sense
rather than their truth-value (“On Sinn and
Bedeutung,” p. 160). Russell, however, does not believe
that true propositions all denote the same object, and so may deal with
indirect speech by addressing informative identities alone.
[18] In this case, “George believes that A has
H” would imply that
“George believes that B has H,” and although the use of
“H” (and of “George”) in these propositions might be
altered through analysis, if A and B are fully analyzed, the implication will
remain valid.
[19] “On Sinn and Bedeutung,” p.
153.
[20] “On Denoting,” pp. 103-4; “Knowledge
By Acquaintance,” pp. 158-9.
[21] This is because all definite descriptions clearly
refer to described entities. The
class of proper names that Russell uses to denote acquainted entities is very
small, however; in “Knowledge by Acquaintance,” he limits the class
to “I” and “this,” and in a footnote added several
years later even rejects the “I” (p. 162).
[22] The shift in terminology here from “acquainted
entity” to “acquainted object” reflects Russell’s
realism, in which acquainted entities such as relations and universals were
considered objects that could serve as the subject of judgments.
[23] By “informative names,” I mean two names
that offer different modes of presentation; a pair consisting of a name and a
symbol stipulated to refer to the same object as the name would not be
considered informative.
[24] Bertrand Russell, The Problems of Philosophy,
1912 (Oxford University Press, 1971), available online at
http://www.ditext.com/russell/russell.html.
[25] The Problems of Philosophy,
http://www.ditext.com/russell/rus10.html.
[26] Ibid.
[27] Russell also accepts logical forms and universals as
acquainted objects (“Knowledge by Acquaintance,” p. 154); the
latter will be addressed below.
[28] While this argument explains the exalted status
afforded sense-data within Russell’s system, it also undercuts his efforts
in “Relations of Sense-Data” to build a physics containing not only
sense-data, but also “sensibilia,” the entities which are of the
same nature as sense-data but are not acquainted. Yet if we are not acquainted with sensibilia, whenever one
is mentioned we must know it through a description composed of sense-data,
which eliminates any explanatory advantage of a system comprised of both
sense-data and sensibilia over one containing sense-data alone. Although Russell would like to
eventually eliminate sensibilia from his system and remove the
“hypothetical scaffolding” (p. 117) — tossing away the
ladder, as it were — it is not clear how this can be done while at the
same time preserving the concept of an object persisting in time.
[29] “The Relation of Sense-Data to Physics,” Mysticism
and Logic, p. 109. Emphasis in
original.
[30] “Relation of Sense-Data,” p. 109.
[31] For one thing, it would be absurd to say that we are
acquainted with the limits unless we can give a very straightforward account of
them; yet if they are known only through description, then they must be
describable in terms of sense-data, which seems equally absurd. Furthermore, the concept of sense-data
as instantaneous would violate Russell’s principle that “no two
instants are contiguous” (“On the Notion of Cause,” 1912, Mysticism
and Logic, p. 135); it would also greatly undermine his project of
representing time as similar in its continuity and completeness to the real
number line. It was this approach
that enabled him to set the work of Weierstrass and Cantor against the
paradoxes that were once thought to attend a time composed of instants (Cf.
“Mathematics and the Metaphysicians,” 1901, Mysticism and Logic,
pp. 63-70).
[32] One might object to this line of reasoning by saying
that the names A and B contain no mode of presentation and offer no
information, and therefore that no need exists to prohibit the proposition
“A = B.” This
objection will be addressed below.
[33] The Problems of Philosophy,
http://www.ditext.com/russell/rus10.html.
[34] The Problems of Philosophy,
http://www.ditext.com/russell/rus9.html.
[35] “Knowledge by Acquaintance,” p. 154.
[36] Russell must be able to treat some predicates as
subject terms in order to avoid the Kerry Paradox, which would make false any
statement of the form “x is a predicate.” While Frege’s defenders are able to claim that such
statements are faults of ordinary speech to be avoided in a perfect language,
Russell has no such excuse.
[37] These similarities need not occur only with the sense
of sight; one might abstract the universal pineapple-taste from a few pieces of pineapple and the universal fruitsnack-taste from a few artificially-flavored fruit snacks and then
later discover, upon further reflection, that the universals are the same; this
is not an assertion that the fruit snacks taste like pineapple, but rather one
about the taste universals themselves.
Because of their origins through separate abstractions, the universals
compared here are not identical because of some mere formalism.
[38] I am assuming here that Russell would accept the
biconditional form of Leibniz’s Law as a sufficient criterion of identity
for universals. Given that formal
identities operate on this principle, no easily apparent reason exists why
informative identities should not do so as well.
[39] “On Sinn and Bedeutung,” p.
154. In suggesting that definite
descriptions be assigned to each proper name, Russell encounters a similar
difficulty to that which faced Frege in determining a proper name’s
sense; specifically, Russell lacked a means of determining, for a given name,
what the correct definite description would be. At one point, Russell suggests that “Julius
Caesar” should be understood as “the man whose name is Julius
Caesar,” on the grounds that
“whatever else I may have forgotten about him, it is plain that when I
mention him I have not forgotten that that was his name”
(“Knowledge by Acquaintance,” p. 160); he even claims that the
statement “one and only one man was called Julius Caesar, and that one was assassinated” is fully analyzed
and “wholly reduced to constituents with which we are acquainted”
(“Knowledge by Acquaintance,” p. 161). However, this view encounters several immediate dangers; one
might speak of “the man whose name was George Sand,” say, or “the man whose name was Nicolas
Bourbaki” (not even the
pseudonym of one individual, but of several) without knowing that those
descriptions are in fact vacuous. Furthermore, any clarification of the process
of naming must involve some reference to those who bestowed the name on an
individual; otherwise, one might interpret “Julius Caesar” to mean
“the man whom I name Julius Caesar” — which seems entirely circular. Yet without an objective route from proper names to
descriptions, Russell provides no guarantee that statements employing proper names can be understood.
[40] There is also the possibility that the universals are
coextensive; however, the finite limits of my experience of particulars falling
under any two universals would give me no grounds on which to infer coextensionality.
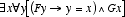 , a structure entirely
without definite descriptions like “the F”; problems of
vacuous descriptions can then be resolved using more familiar logical
techniques. “The present king of France is bald” would become
the sentence
, a structure entirely
without definite descriptions like “the F”; problems of
vacuous descriptions can then be resolved using more familiar logical
techniques. “The present king of France is bald” would become
the sentence 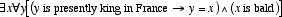 , which, because
there
is no such x, can be clearly determined to be false. To resolve the
status of sentences such as “Apollo is bald,” instances of
“Apollo” can be replaced with a corresponding definite
description — Russell suggests “the sun-god”[7]— and the sentence interpreted
using previously outlined rules. Of course, there is a need for
iteration of this procedure if the definite description contains new
proper names, and there must be a guarantee that the analysis will cease
after a finite number of iterations, but these will be dealt with
below. What is important to note at this point is that as proper
names and definite descriptions are eliminated, the danger of vacuity
disappears, and the dilemmas noted above lose their relevance.
, which, because
there
is no such x, can be clearly determined to be false. To resolve the
status of sentences such as “Apollo is bald,” instances of
“Apollo” can be replaced with a corresponding definite
description — Russell suggests “the sun-god”[7]— and the sentence interpreted
using previously outlined rules. Of course, there is a need for
iteration of this procedure if the definite description contains new
proper names, and there must be a guarantee that the analysis will cease
after a finite number of iterations, but these will be dealt with
below. What is important to note at this point is that as proper
names and definite descriptions are eliminated, the danger of vacuity
disappears, and the dilemmas noted above lose their relevance.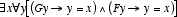 . The only identities here are
between bound
variables, where no mode of presentation is at issue and no issue of
informative identity can arise.
. The only identities here are
between bound
variables, where no mode of presentation is at issue and no issue of
informative identity can arise.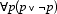 ) with propositions rather than
truth
values, and a
proposition neither true nor false would therefore violate the law of the
excluded middle.
) with propositions rather than
truth
values, and a
proposition neither true nor false would therefore violate the law of the
excluded middle. 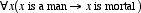 .
.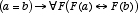 .
.